Skip to content

Commit eed725b

Browse files
aubertcaubertc
committed
Working on complexity notes.
1 parent 7cab7c5 commit eed725b

File tree

3 files changed

+261
-107
lines changed

3 files changed

+261
-107
lines changed

‎source/code/projects/GrowthMagnitudes/GrowthMagnitudes/Program.cs

Lines changed: 177 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,177 @@
1+
using System;
2+
using System.IO;
3+
4+
class Program
5+
{
6+
// We implement our own factorial function:
7+
static int factorial(int n)
8+
{
9+
if (n == 0)
10+
return 1;
11+
else
12+
return checked(factorial(n - 1) * n);
13+
}
14+
15+
static void Main()
16+
{
17+
// As a reminder, this is the "biggest" integer
18+
// value C# can handle:
19+
Console.WriteLine(int.MaxValue);
20+
// 2,147,483,647
21+
22+
// Remember that it's easy to trick C# into
23+
// overflowing:
24+
int x = int.MaxValue;
25+
int y = x + 1;
26+
Console.WriteLine(y);
27+
28+
// Hence, we use the "checked" keyword
29+
// to force C# to check that no overflow
30+
// occurs:
31+
try
32+
{
33+
y = checked(x + 1);
34+
}
35+
catch (System.OverflowException)
36+
{
37+
Console.WriteLine("An overflow exception was thrown.");
38+
}
39+
40+
// Now we illustrate various growth
41+
// magnitude. Each "function" will have its
42+
// input grow linearly, and we will count
43+
// which input size makes the function
44+
// outputs something that is bigger than
45+
// the "biggest" integer value.
46+
47+
// Factorial
48+
int inputfact = 0;
49+
int outputfact;
50+
try
51+
{
52+
while (true)
53+
{
54+
inputfact++;
55+
outputfact = checked(factorial(inputfact));
56+
}
57+
}
58+
catch (System.OverflowException)
59+
{
60+
Console.WriteLine("Factorial: an overflow exception was thrown once input reached " + inputfact + ".");
61+
// Factorial: an overflow exception was thrown once input reached 13.
62+
// 13! = 6,227,020,800
63+
}
64+
65+
// Exponential
66+
int inputexp = 0;
67+
int outputexp;
68+
try
69+
{
70+
while (true)
71+
{
72+
inputexp++;
73+
checked
74+
{
75+
outputexp = (int)Math.Pow(2, inputexp);
76+
}
77+
}
78+
}
79+
catch (System.OverflowException)
80+
{
81+
Console.WriteLine("Exponential: an overflow exception was thrown once input reached " + inputexp + ".");
82+
// Exponential: an overflow exception was thrown once input reached 31.
83+
// 2^31 = 2,147,483,648
84+
}
85+
86+
// Cubic
87+
int inputcubic = 0;
88+
int outputcubic;
89+
try
90+
{
91+
while (true)
92+
{
93+
inputcubic++;
94+
checked
95+
{
96+
outputcubic = (int)Math.Pow(inputcubic, 3);
97+
}
98+
}
99+
}
100+
catch (System.OverflowException)
101+
{
102+
Console.WriteLine("Cubic: an overflow exception was thrown once input reached " + inputcubic + ".");
103+
// Cubic: an overflow exception was thrown once input reached 1291.
104+
// 1,291^3 = 2,151,685,171
105+
}
106+
107+
// Quadratic
108+
int inputquad = 0;
109+
int outputquad;
110+
try
111+
{
112+
while (true)
113+
{
114+
inputquad++;
115+
checked
116+
{
117+
outputquad = (int)Math.Pow(inputquad, 2);
118+
}
119+
}
120+
}
121+
catch (System.OverflowException)
122+
{
123+
Console.WriteLine("Quadratic: an overflow exception was thrown once input reached " + inputquad + ".");
124+
// Quadratic: an overflow exception was thrown once input reached 46341.
125+
// 46,341^2 = 2,147,488,281
126+
}
127+
128+
// Linearithmic
129+
int inputlinearith = 81703000; // We do not start at 0 to save some time
130+
int outputlinearith;
131+
try
132+
{
133+
while (true)
134+
{
135+
inputlinearith++;
136+
checked
137+
{
138+
outputlinearith = (int)(inputlinearith * Math.Log(inputlinearith, 2));
139+
}
140+
}
141+
}
142+
catch (System.OverflowException)
143+
{
144+
Console.WriteLine("Linearithmic: an overflow exception was thrown once input reached " + inputlinearith + ".");
145+
// Linearithmic: an overflow exception was thrown once input reached 81703409.
146+
// 81,703,409 * (log(81,703,409)) = 81,703,409 * 26.2838929389692 = 2,147,483,654.90481
147+
}
148+
149+
// Linear
150+
int inputlinear = 2147483640; // We do not start at 0 to save some time
151+
int outputlinear;
152+
try
153+
{
154+
while (true)
155+
{
156+
checked
157+
{
158+
inputlinear++;
159+
outputlinear = inputlinear;
160+
}
161+
}
162+
}
163+
catch (System.OverflowException)
164+
{
165+
Console.WriteLine("Linear: an overflow exception was thrown once input reached " + inputlinear + ".");
166+
// Linear: an overflow exception was thrown once input reached 2147483647.
167+
// 2,147,483,647 is Max.IntValue
168+
}
169+
170+
// Logarithmic
171+
double inputlog = Double.MaxValue - 1;
172+
// This is 1.7976931348623157E+308;
173+
double outputlog= Math.Log(inputlog, 2);
174+
Console.WriteLine("Logarithmic: log of " + inputlog + " is " + outputlog + ".");
175+
// Logarithmic: log of 1.79769313486232E+308 is 1024.
176+
}
177+
}

‎source/code/snippets/complexity.cs

Lines changed: 0 additions & 95 deletions
This file was deleted.

‎source/docs/programming_and_computer_usage/complexity.md

Lines changed: 84 additions & 12 deletions
Original file line numberDiff line numberDiff line change
@@ -1,22 +1,94 @@
1-
# Some Notes on Complexity
1+
# Complexity
2+
3+
## What makes a program "better"?
4+
5+
There are multiple ways of measuring if a program is "better" than an other, assuming they perform similar functions:
6+
7+
- Correctness: a program not producing the correct output is worst than a program that is always correct,
8+
- Security: a program leaking personal information or infesting your computer will always be worst than one that does not,
9+
- Memory: the less a program requires memory to be installed and to run efficiently, the better.
10+
- Time: the faster the program produces the output, the better.
11+
- Other measures: ergonomics, cost, compatibility with operating systems, licence, network efficiency, may also come into play to decide which program is "best".
12+
13+
Some criteria may be subjective (usability, for example), but some can be approach objectively: in a first approximation, memory (also called "space") and time are the two preferred measures.
14+
15+
## Orders of magnitude in growth rates
16+
17+
### Principles
18+
19+
When measuring space or time, it is important to take the size of the input into account: that a word-processing software can open a document containing 1 word in 0.0001 second is no good if it takes hours to open a 10 pages document.
20+
21+
Hence, algorithms and programs are classified according to their *growth rates*, how "fast" their run time or space requirements grow when the input size grows.
22+
This growth rate is classified according to ["orders"](https://en.wikipedia.org/wiki/Big_O_notation#Orders_of_common_functions), using the [*Big O notation*](https://en.wikipedia.org/wiki/Big_O_notation), whose definition follows:
23+
24+
Using $|\cdot|$ to denote the absolute value, we write:
25+
26+
$$f(x) = O(g(x))$$
27+
28+
if there exists positive numbers $n$ and $x_0$ such that
29+
30+
$$|f(x)| \leqslant M |g(x)|$$
31+
32+
for all $x \geqslant x_0$.
33+
34+
### Common orders of magnitude
35+
36+
Using $c>1$ for "a constant", $n$ for the size of the input and $\log$ for logarithm in base $2$, we have the following common [orders of magnitude](https://en.wikipedia.org/wiki/Big_O_notation#Orders_of_common_functions):
37+
38+
- constant ($O(c)$),
39+
- logarithmic ($O(\log n)$),
40+
- linear ($O(n)$),
41+
- [linearithmic](https://en.wikipedia.org/wiki/Time_complexity#Quasilinear_time) ($O(n \times \log(n)))$),
42+
- polynomial ($O(n^c)$), which includes
43+
- quadratic ($O(n^2)$),
44+
- cubic ($O(n^3)$),
45+
- exponential ($O(c^n)$),
46+
- factorial ($O(n!)$).
47+
48+
### Simplifications
49+
50+
In typical usage the $O$ notation is *asymptotical* (we are interested in very large values), which means that only the contribution of the terms that grow "most quickly" is relevant. Hence, we can use the following rules:
51+
52+
- If $f(x)$ is a sum of several terms, if there is one with largest growth rate, it can be kept, and all others omitted.
53+
- If $f(x)$ is a product of several factors, any constants (factors in the product that do not depend on $x$) can be omitted.
54+
55+
There are additionaly some very useful [properties of the big O notation](https://www.geeksforgeeks.org/dsa/properties-of-asymptotic-notations/):
56+
57+
- Reflexivity: $f(n) = O(f(n))$,
58+
- Transitivity: $f(n) = O(g(n))$ and $g(n) = O(h(n))$ implies $f(n) = O(h(n))$,
59+
- Constant factor: $f(n) = O(g(n))$ and $c > 1$ implies $c\times f(n) = O(g(n))$,
60+
- Sum rule: $f(n) = O(g(n))$ and $h(n) = O(k(n))$ implies $f(n) + h(n) = O(\max (g(n), k(n))$,
61+
- Product rule: $f(n) = O(g(n))$ and $h(n) = O(k(n))$ implies $f(n) \times h(n) = O(g(n) \times k(n))$,
62+
- Composition rule: $f(n) = O(g(n))$ and $g(n) = O(h(n))$ implies $f(g(n)) = O(h(n))$.
63+
64+
$$
65+
\begin{align*}
66+
f(n) & = O(f(n)) \tag{Reflexivity}\\
67+
f(n) & = O(f(n)) \text{Reflexivity}
68+
\end{align*}
69+
$$
70+
71+
<!--
72+
Example 1: f(n) = 3n2 + 2n + 1000Logn + 5000
73+
After ignoring lower order terms, we get the highest order term as 3n2
74+
After ignoring the constant 3, we get n2
75+
Therefore the Big O value of this expression is O(n2)
76+
77+
Example 2 : f(n) = 3n3 + 2n2 + 5n + 1
78+
Dominant Term: 3n3
79+
Order of Growth: Cubic (n3)
80+
Big O Notation: O(n3)
81+
-->
82+
83+
284

385
Have a look at the [Big-O complexity chart](https://www.bigocheatsheet.com/):
486

587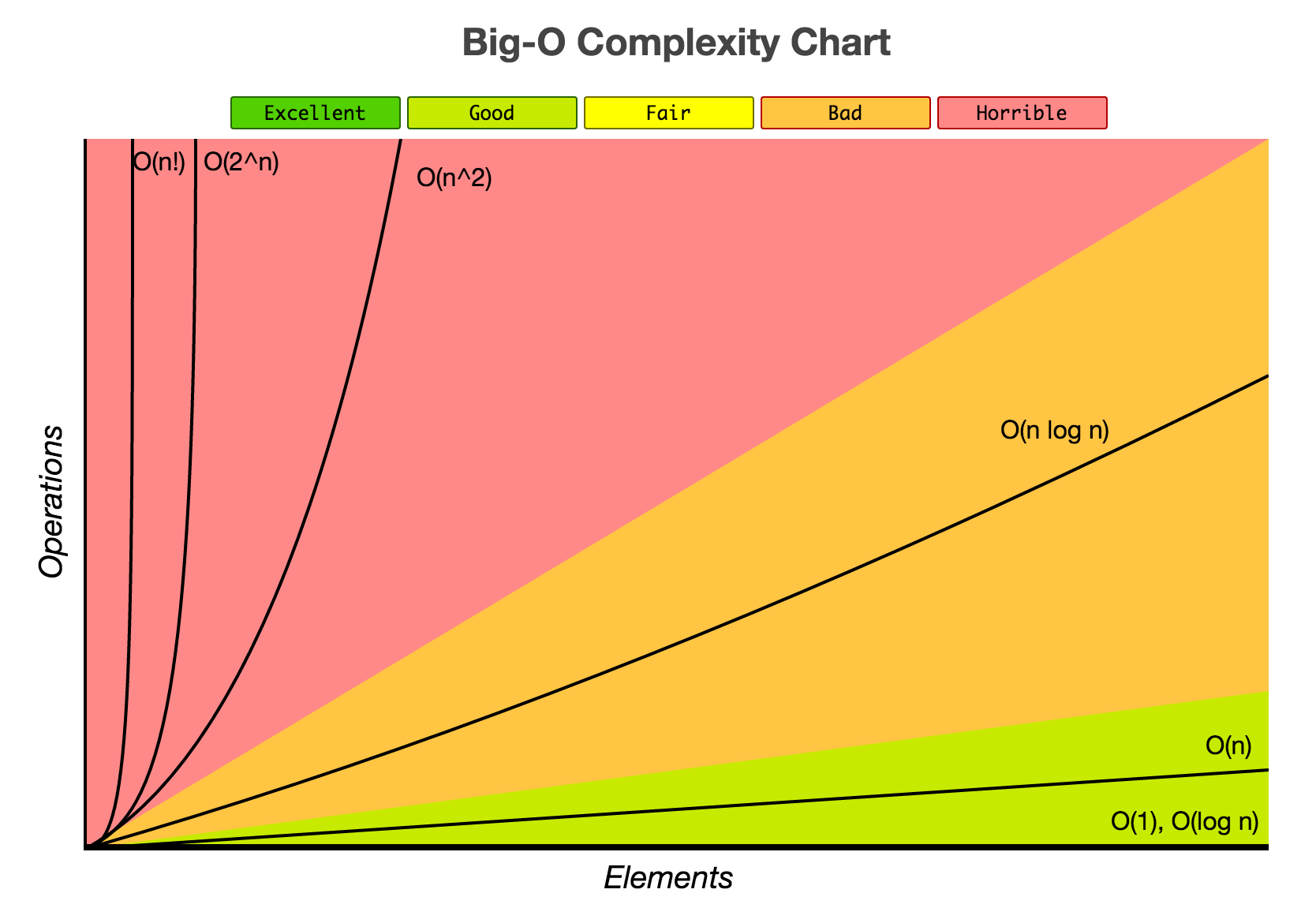
![Big-O Complexity Chart](https://www.bigocheatsheet.com/img/big-o-complexity-chart.png)
688

7-
A function [has an order](https://en.wikipedia.org/wiki/Big_O_notation#Orders_of_common_functions), it can be for example
8-
9-
- constant (O(c)),
10-
- logarithmic (O(log n)),
11-
- linear (O(n)),
12-
- [linearithmic](https://en.wikipedia.org/wiki/Time_complexity#Quasilinear_time) (O(n log n)),
13-
- quadratic (O(n^2)),
14-
- cubic (O(n^3)),
15-
- exponential (O(c^n)),
16-
- factorial (O(n!)).
1789

1890
This can make a *very* significant difference, as exemplified in the following code:
1991

2092
```
21-
!include code/snippets/complexity.cs
93+
!include code/projects/GrowthMagnitudes/GrowthMagnitudes/Program.cs
2294
```

0 commit comments

Comments
 (0)